Are Alternate Interior Angles Always Congruent

Corresponding angles lie in the same position at each intersection.

Are alternate interior angles always congruent. In our case we have that the alternate interior angles are congruent that is we have that there are two pairs of alternate interior angles that are congruent and that together one angle from each pair forms a straight angle as you go along the lines. We see two parallel lines and a third line transversal intersecting. Whats people lookup in this blog.

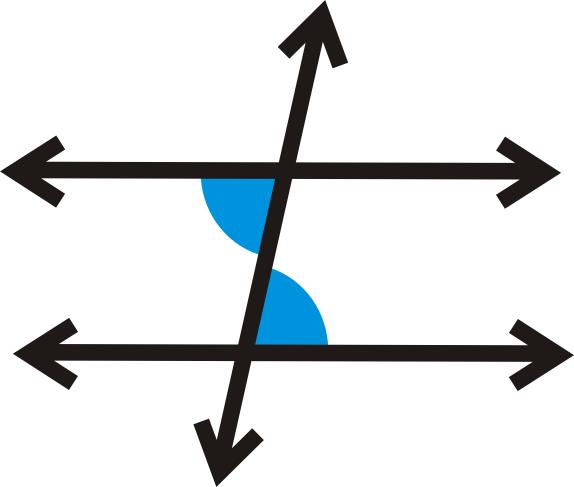
Alternate interior angles are congruent. When two lines are crossed by another line called the transversal alternate interior angles are a pair of angles on the inner side of each of those two lines but on opposite sides of the transversal. Alternate interior angles are always congruent.

Alternate interior angle theorem the alternate interior angles theorem states that when two parallel lines are cut by a transversal the resulting alternate interior angles are congruent. Alternate interior angles are always congruent true or false. This is illustrated in the image below.

Looking at the illustration above the two teal colored lines are parallel to each other. Learn vocabulary terms and more with flashcards games and other study tools. Mrwadeturner t2 corresponding and alt interior proving alternate interior angles are congruent the same angles and parallel lines mathbitsnotebook geo ccss math untitled doent.

Start studying always sometimes or never geometry. In geometry a transversal is a line that passes through two lines in the same plane at two distinct points transversals play a role in establishing whether two other lines in the euclidean plane are parallel the intersections of a transversal with two lines create various types of pairs of angles. This means that the sum of the angles on each side of the transversal.

Learn about alternate interior angles. The lines are parallel if alternate interior alternate exterior or corresponding angles are congruent. Alternate interior angles lie between the lines cut by the transversal.